stable sorting algorithm
크기가 같은 데이터가 정렬 이후에도 입력된 순서 그대로 유지되는 알고리즘
ex) Merge sort, Insertion Sort, Bubble Sort, Cocktail Shaker Sort
In-Place algorithm
입력 데이터를 저장하는 메모리 이외는 상수 크기의 메모리만 필요한 알고리즘
ex) Heap sort, Insertion sort, Selection sort, Shell sort, Bubble sort, Comb Sort, Cocktail shaker sort
Bubble sort
인접한 두 숫자를 비교하여 두 수의 정렬순서가 맞지 않는 경우에는 교환(swap)한다.
(stable, in-place)
public static void bubbleSort(int[] arr){
for (int i = 1; i < arr.length; i++) {
for (int j = 1; j <= arr.length - i; j++) {
if(arr[j-1] > arr[j]) swap(arr, j-1, j);
}
}
}
public static void bubbleSortImproved1(int[] arr){
for (int i = 1; i < arr.length; i++) {
boolean swapped = false;
for (int j = 1; j <= arr.length - i; j++) {
if(arr[j-1] > arr[j]){
swap(arr, j-1, j);
swapped = true;
}
}
//한번도 바뀌지 않았다면 이미 정렬되어 있는 것이므로 더 진행할 필요가 없음.
if(swapped == false) break;
}
}
public static void bubbleSortImproved2(int[] arr){
int lastSwappedPos = arr.length;
while(lastSwappedPos > 0){
int swappedPos = 0;
for (int i = 1; i < lastSwappedPos; i++) { //이전에 교환한 곳까지만 진행한다.
if(arr[i-1] > arr[i]){
swap(arr, i-1, i);
swappedPos = i;
}
}
lastSwappedPos = swappedPos;
}
}Bubble sort에서 토끼 데이터(왼쪽에 있는 큰 데이터)들은 몇번만 pass를 거쳐도 빠르게 제 위치로 이동하는 반면, 거북이 데이터(오른쪽에 있는 작은 데이터)들은 매우 느리게 제 위치로 이동한다.
이런 문제점을 개선한 것이 바로 Cocktail Shaker sort, Comb sort이다.
Cocktail Shaker sort - O(n^2)
Bidirectional bubble sort라고도 불리며, bubble sort의 단점을 개선하여 거북이 데이터를 빠르게 제 위치로 이동시킨다.
bubble sort의 각 pass를 한번은 왼쪽에서 오른쪽으로, 그 다음에는 오른쪽에서 왼쪽으로 실행하며 정렬하는 방법이다.
(stable, in-place)

Comb sort
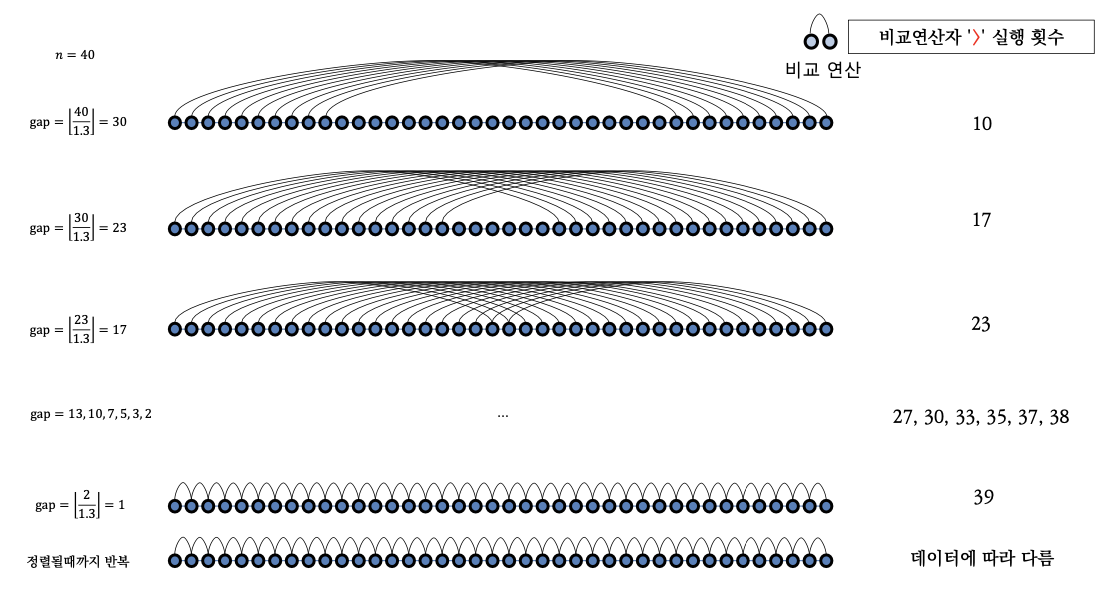
bubble sort에서 발생하는 거북이 데이터 문제를 gap 크기를 늘림으로서 해결한다.
비교하는 두 데이터 사이의 거리인 gap을 1보다 크게 하여 시작하고, 각 pass가 진행됨에 따라 gap의 크기를 줄여간다.
comb sort의 효율성은 gap의 크기에 따라 달라진다. (권장되는 k값: 1.3)
(not stable, in-place)
public static void combSort(int[] arr){
double gap = arr.length;
double shrink = 1.3;
boolean sorted = false;
while (sorted==false){
gap = Math.floor(gap/shrink);
if(gap<=1){
gap = 1;
sorted = true;
}
int i = 0;
while (i+gap < arr.length){
if(arr[i] > arr[i+(int)gap]){
swap(arr, i, i+(int)gap);
sorted = false;
}
i++;
}
}
}
Selection sort
우선 데이터를 두 부분으로 나누어 왼쪽에는 정렬된 데이터, 오른쪽에는 정렬되지 않은 데이터를 둔다.
그리고 오른쪽 정렬되지 않은 데이터 중 제일 작은 데이터를 검색하여 선택하고, 이를 오른쪽 데이터의 제일 앞 숫자와 교환한다.
각 pass 마다 오른쪽에서 제일 작은 데이터가 선택되어 제 위치로 옮겨진다.
(not stable, in-place)

public static void selectionSort(int[] arr){
for (int i = 0; i < arr.length - 1; i++) {
int jMin = i;
for (int j = i+1; j < arr.length; j++) {
if(arr[jMin] > arr[j]){
jMin = j;
}
}
if(jMin != i) swap(arr, jMin, i);
}
}
Insertion sort
데이터를 두 부분으로 나누어 왼쪽에는 정렬된 데이터, 오른쪽에는 정렬되지 않은 데이터를 두는 것까지는 선택정렬과 동일하나,
오른쪽 데이터의 제일 앞 숫자를 왼쪽 정렬된 데이터의 제 위치에 삽입하는 방식으로 정렬된다는 점에서 차이가 있다.
이때 중간의 모든 데이터는 오른쪽으로 한칸씩 이동한다.
(stable, in-place)

public static void insertionSort(int[] arr){
for (int i = 1; i < arr.length; i++) {
for (int j = i; j>0 && arr[j-1]>arr[j]; j--) {
swap(arr, j-1, j);
}
}
}insertion sort에서도 거북이 데이터 문제는 발생하는데, 이를 보완한 것이 shell sort이다.
Shell sort
insertion sort를 기본으로 하지만, gap의 크기를 크게 시작해 점점 줄여나가는 방식으로 정렬한다.
bubble sort의 보완 알고리즘이 comb sort인 것처럼, insertion sort의 보완 알고리즘은 shell sort이다.

public static void shellSort(int[] arr){
int shrink = 2;
int gap = 2/shrink;
while (gap>0){
for (int i = gap; i < arr.length; i++) {
int tmp = arr[i];
int jTmp = i;
for (int j = i; j>=gap && arr[j-gap]>tmp; j-=gap) {
jTmp = j-gap;
arr[j] = arr[j-gap];
}
arr[jTmp] = tmp;
}
gap /= shrink;
}
}
'자료구조' 카테고리의 다른 글
| 재귀 알고리즘 예시 (+피보나치 분할정복 방법) (0) | 2023.10.18 |
|---|---|
| 재귀 알고리즘 (0) | 2022.07.17 |
| 큐(Queue) (0) | 2022.07.16 |
| 스택(Stack) (0) | 2022.07.16 |
| 배열검색 (이진검색) (0) | 2022.07.15 |